哪些运动方程对工业机器人很重要？

运动学模型是机器人运动的数学表示，它侧重于元件之间的几何关系，而忽略了影响运动的外力。运动学模型用于规划和控制工业机器人的路径。 

正向运动学根据机器人手臂中每个关节的角度确定末端执行器的当前位置和方向。计算使用一系列变换矩阵，其中包含关节角度、长度和偏移参数。

变换矩阵从机器人基础到末端执行器按顺序相乘。结果是三维坐标中的位置和末端执行器的方向（以角度表示）。反向运动学反转了该过程，根据末端执行器的位置确定所需的关节角度，如图 1 所示。

图 1.使用正向或反向运动学定义机器人关节位置。（图片：MathWorks）)

Denavit-Hartenberg 公约

Denavit-Hartenberg （DH） 约定是表示机器人几何和关节角度的标准化方法。它详细介绍了如何将坐标系附加到机器人中的关节，从而定义相邻关节之间的相对位置和方向。

如图 2 所示，每个关节或链接由四个参数描述，包括链接长度 （a）、链接角度 （θ）、链接偏移 （d） 和链接扭曲 （α）。这四个参数用于计算每个关节的转换矩阵。矩阵可以相乘以确定从机器人底座到末端执行器的整体变换。控制系统使用 DH 参数来计算所需的关节角度，以实现所需的末端执行器姿势。

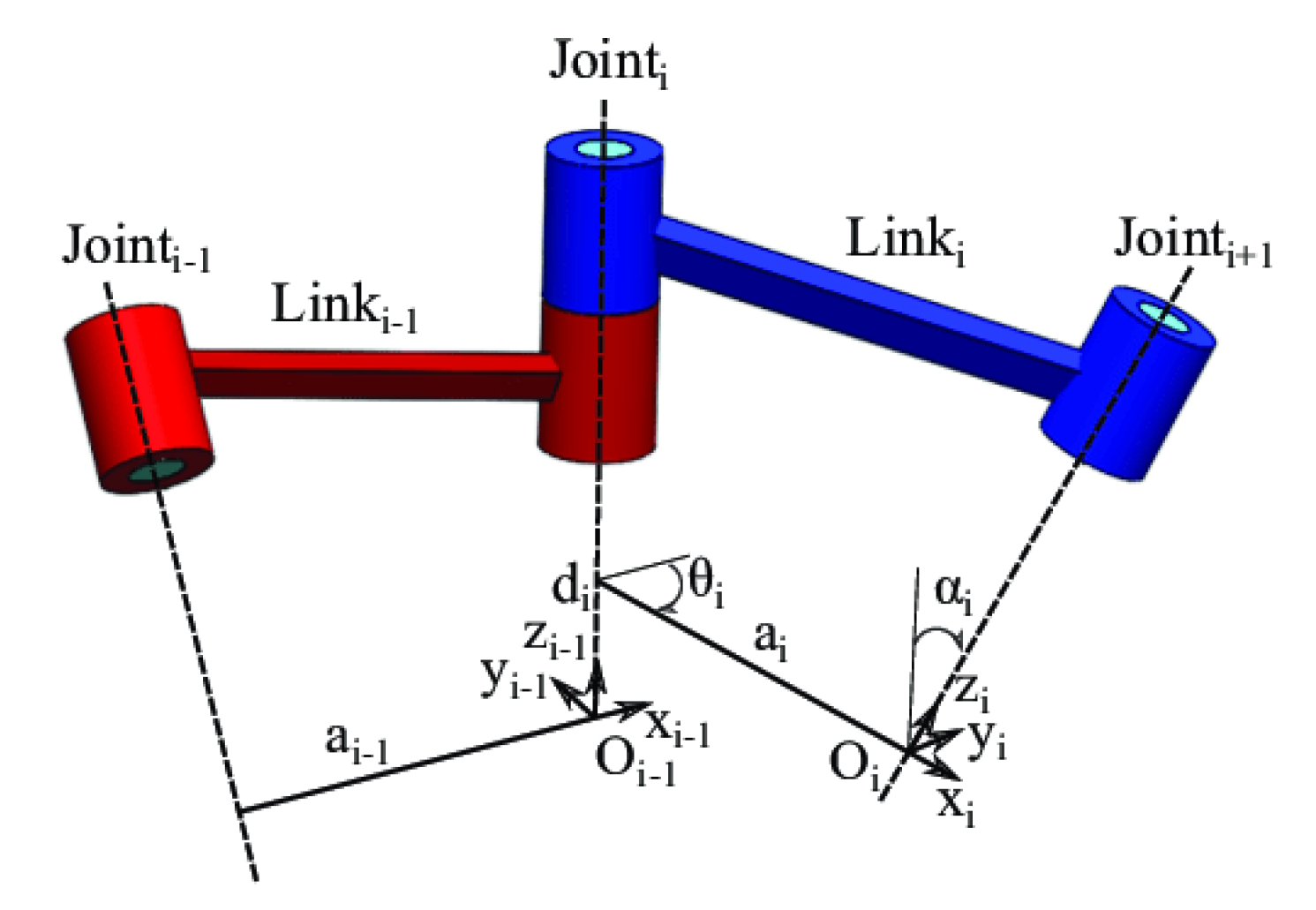图 2.DH 参数示例。（图片：MDPI 传感器)

雅可比矩阵

DH 约定可以与雅可比矩阵一起使用，以将联合速度与末端执行器速度相关联。关节速度可以描述旋转关节的关节旋转速度，以及棱柱关节关节的关节伸展或收缩的速度。

雅可比矩阵 （J） 是偏导数矩阵，用于描述关节速度和末端执行器速度之间的关系。在机器人控制系统中，J 用于将关节速度映射到末端执行器的速度。

换位 J 允许计算在末端执行器上产生所需力所需的关节扭矩。在运动规划中，J 用于识别和避免机器人失去自由和精确移动能力的奇点。当 J 的行列式变为零时，就会出现奇点。

奇异

在奇点中，关节角度和末端执行器位置之间的数学关系会断开，机器人会失去一个或多个自由度。当多个关节以阻止机器人向一个或多个方向移动的方式对齐时，就会出现奇点。这可能导致失控、不稳定或动作抽搐。通过仔细设计运动轨迹，可以避免奇点配置。

可作性

奇点是有限可纵性的一种形式。Manipulability （可作性） 衡量机器人根据当前关节配置更改末端执行器位置的程度。可纵性是使用 J 的奇异值分解来计算可纵性椭球体的。

可纵性椭球体直观地表示机器人向不同方向移动的能力。体积较大的椭球体表示更高的可作性。椭球体轴的比率接近 1 表示在所有方向上的可纵性相等，称为各向同性可纵性。较大的比率表明奇点正在逼近。

总结

运动方程用于确定从一个姿势移动到另一个姿势的最佳轨迹，并避免可能限制机器人运动的奇点等困难。DH 约定是表示机器人的几何图形和关节角度的标准化方法。雅可比矩阵提供了用于优化机器人运动的计算框架。